Distribution Rules Under Dichotomous Preferences: Two Out of Three Ain’t Bad
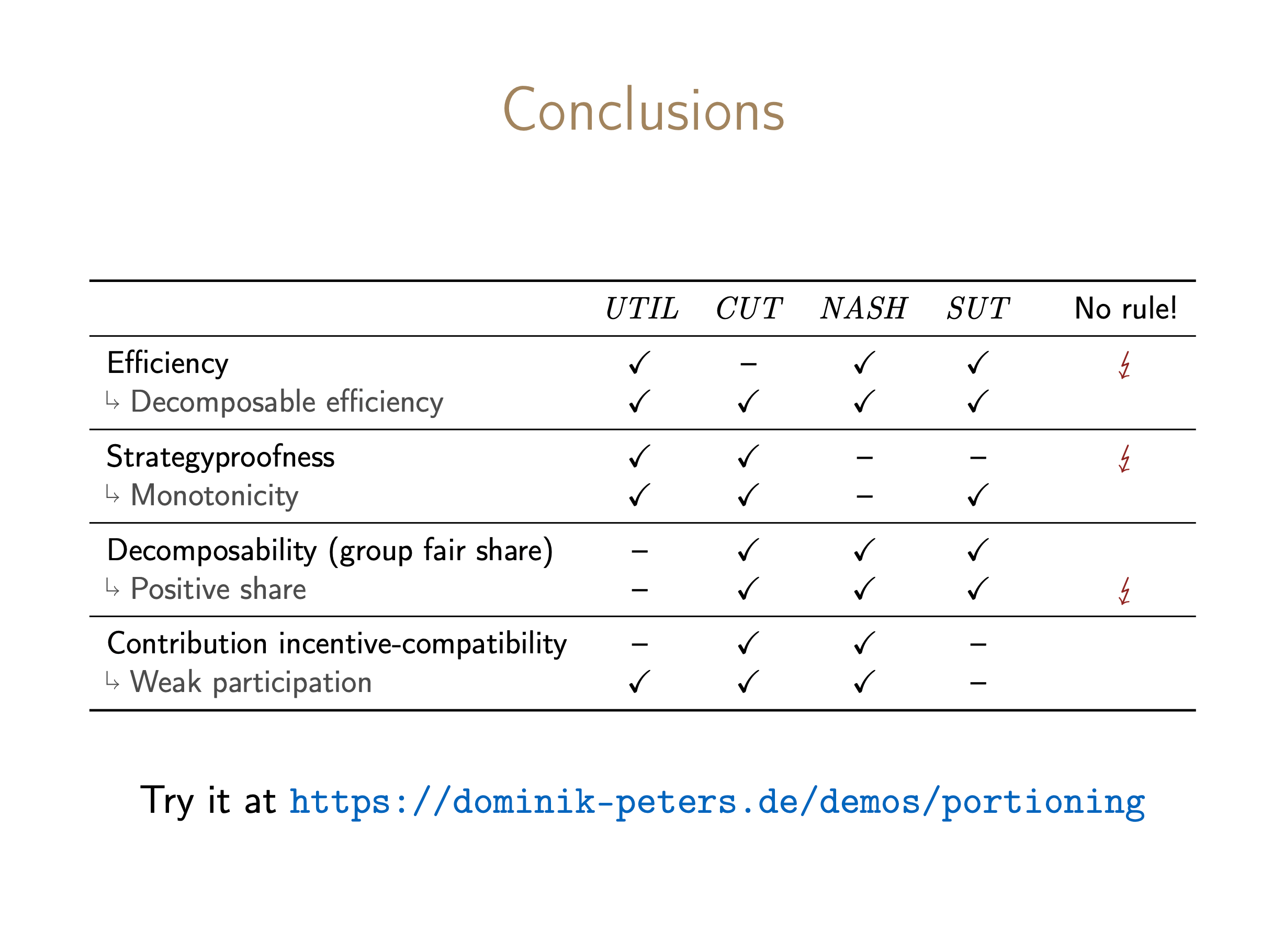
We consider a setting in which agents contribute amounts of a divisible resource (such as money or time) to a common pool, which is used to finance projects of public interest. How the collected resources are to be distributed among the projects is decided by a distribution rule that takes as input a set of approved projects for each agent. An important application of this setting is donor coordination, which allows philanthropists to find an efficient and mutually agreeable distribution of their donations. We analyze various distribution rules (including the Nash product rule and the conditional utilitarian rule) in terms of classic as well as new axioms, and propose the first fair distribution rule that satisfies efficiency and monotonicity. Our main result settles a long-standing open question of Bogomolnaia, Moulin, and Stong (2005) by showing that no strategyproof and efficient rule can guarantee that at least one approved project of each agent receives a positive amount of the resource. The proof reasons about 386 preference profiles and was obtained using a computer-aided method involving SAT solvers.
