The Distribution of Optimal Strategies in Symmetric Zero-sum Games
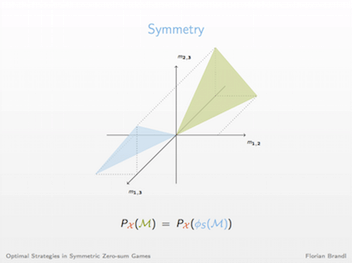
Given a skew-symmetric matrix, the corresponding two-player symmetric zero-sum game is defined as follows: one player, the row player, chooses a row and the other player, the column player, chooses a column. The payoff of the row player is given by the corresponding matrix entry, the column player receives the negative of the row player. A randomized strategy is optimal if it guarantees an expected payoff of at least 0 for a player independently of the strategy of the other player. We determine the probability that an optimal strategy randomizes over a given set of actions when the game is drawn from a distribution that satisfies certain regularity conditions. The regularity conditions are quite general and apply to a wide range of natural distributions.
