A Natural Adaptive Process for Collective Decision-Making
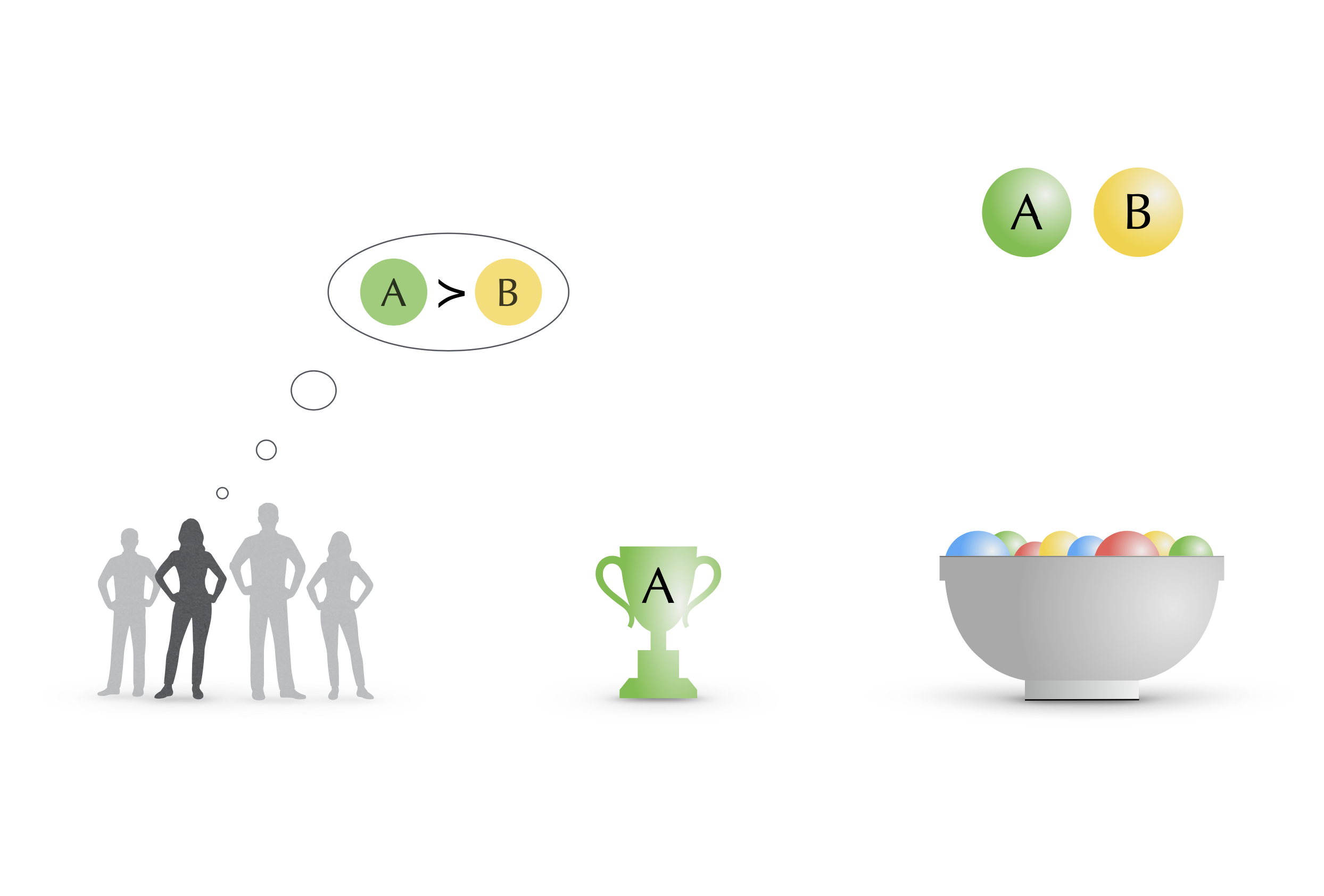
Consider an urn filled with balls, each labeled with one of several possible collective decisions. Now, let a random voter draw two balls from the urn and pick her more preferred as the collective decision. Relabel the losing ball with the collective decision, put both balls back into the urn, and repeat. Once in a while, relabel a randomly drawn ball with a random collective decision. We prove that the empirical distribution of collective decisions produced by this process approximates a maximal lottery, a celebrated probabilistic voting rule proposed by Peter C. Fishburn (Rev. Econ. Stud., 51(4), 1984). In fact, the probability that the collective decision in round n is made according to a maximal lottery increases exponentially in n. The proposed procedure is more flexible than traditional voting rules and bears strong similarities to natural processes studied in biology, physics, and chemistry as well as algorithms proposed in machine learning.
